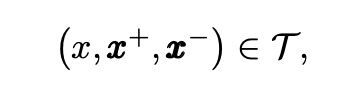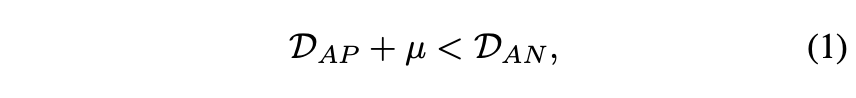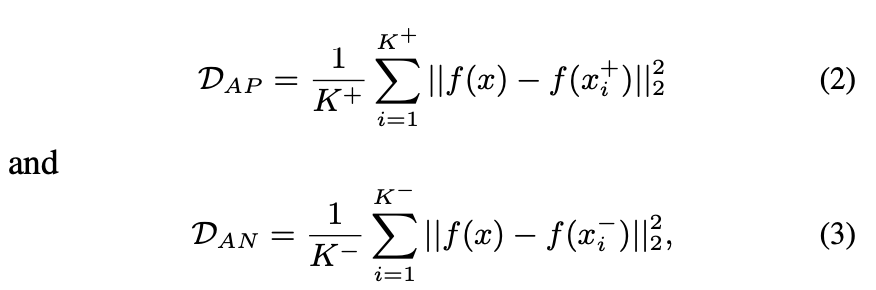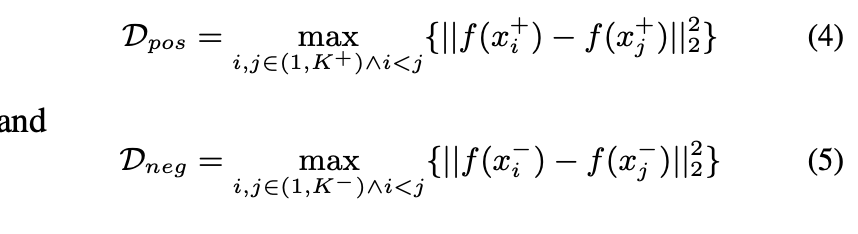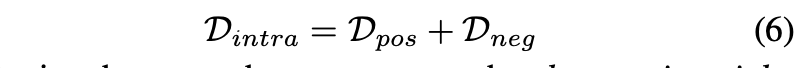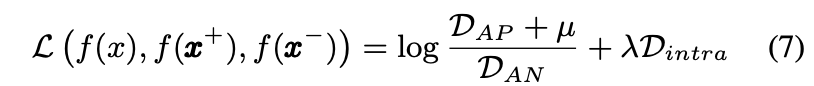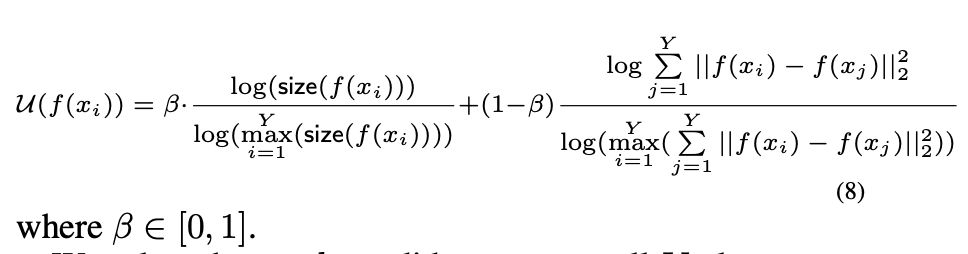关键词:多变量时间序列,时间序列分类
在本文中,我们提出了一个名为ShapeNet的新型模型,该模型将不同长度的小波候选者嵌入到统一的空间中,以进行小波选择。该网络使用聚类三元组损失进行训练,该损失考虑了锚点与多个正(负)样本之间的距离以及正(负)样本之间的距离,这对于收敛非常重要。我们计算有代表性的和多样化的最终小波,而不是直接使用所有小波嵌入进行模型构建,以避免很大一部分非歧视性小波候选。我们已经使用UEA多元时间序列数据集在ShapeNet上进行了具有竞争性的最新技术和基准测试方法的实验。结果表明,ShapeNet的准确性是所有比较方法中最好的。此外,我们通过两个案例研究说明了小波的可解释性。
1 介绍
MTSC(多元时间序列分类)挑战:
·多元时间序列有多个变量,候选小波可能是大量或异质(一个变量有不同的候选小波)的。
·不同变量的候选小波可能有不同的长度。
·大多数模型是黒盒模型。
贡献:
本文提出了shapeNet方法,提高了分类的准确性并给了可解释的分类结果。
首先,我们提出了多长度输入扩张因果卷积神经网络(Mdc-CNN),该网络增强了Dc-CNN,将不同长度和不同变量的小波候选对象嵌入到统一空间中(小波嵌入)。我们采用了扩展卷积,这使得序列的接受域指数增大从而能够处理长期依赖性,而不会使模型的复杂性激增。因果卷积仅用于对当前时间之前的时间序列进行卷积,以确保将来的值不会影响当前值。
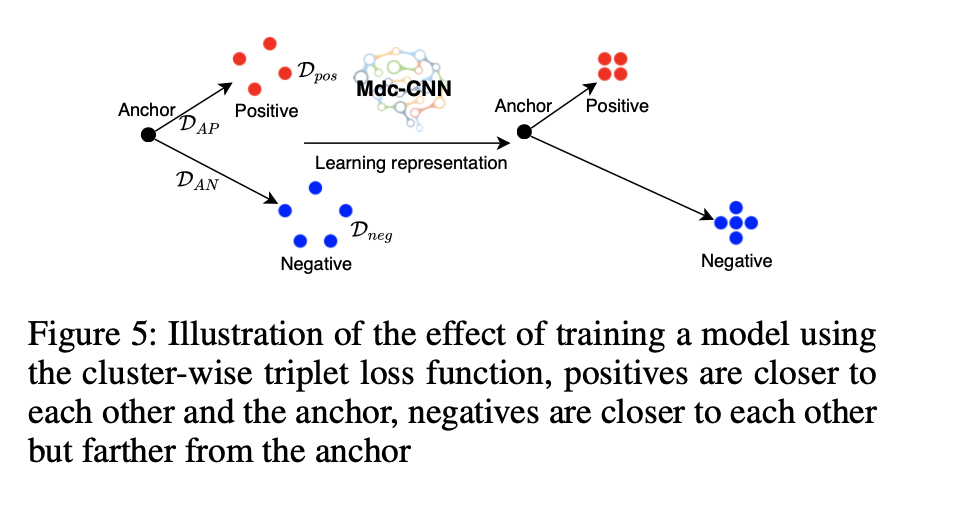
此外,我们提出了一种用于训练Mdc-CNN的聚类三元组损失函数,该函数考虑了集群内/集群间度量学习以加速收敛和提高稳定性。
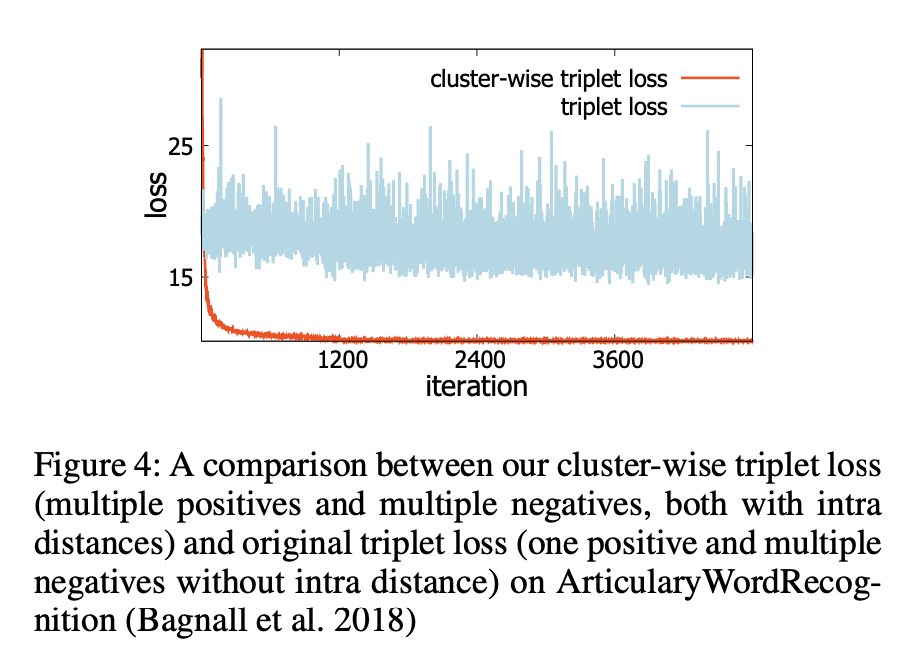
我们的聚类三元组损失不仅将多个正样本和多个负样本作为输入,而且还计算了它们之间的距离。相比之下,先前的三元组损失仅涉及一个正样本和一个负样本。我们的损失函数更加健壮,可以更快地确定小波嵌入和收敛(请参见图4)。据我们所知,本文是第一个使用神经网络发现MTS中小波的方法。
其次,我们避免直接喂入许多小波候选对象(通过使用Mdc-CNN的嵌入学习进行编码)来建立分类器。 我们首先聚簇小波候选嵌入。 然后,我们提出一个效用函数,以选择与大簇的质心接近且与其他聚类质心不同的前k个候选对象,这为我们提供了具有代表性和多样化的最终小波。
然后,我们采用首先正式定义的多元小波变换(MST)。 具体来说,给定一个多元时间序列,我们计算其到同一变量的候选小波的距离,以获得MST表示。
最后,由于有MST表示,我们可以轻松地学习分类模型。 在本文中,我们采用线性支持向量机,这使我们能够可视化不同变量的小波如何分离不同类别的时间序列。
我们在UEA MTS档案库上进行实验。 结果表明,就精度而言,ShapeNet是最新方法中最好的基准。 我们注意到ShapeNet在30个数据集中的14个数据集中提供了最佳性能。 我们介绍了人类动作识别和ECG数据的两种情况,以说明小波如何给出分类的可解释。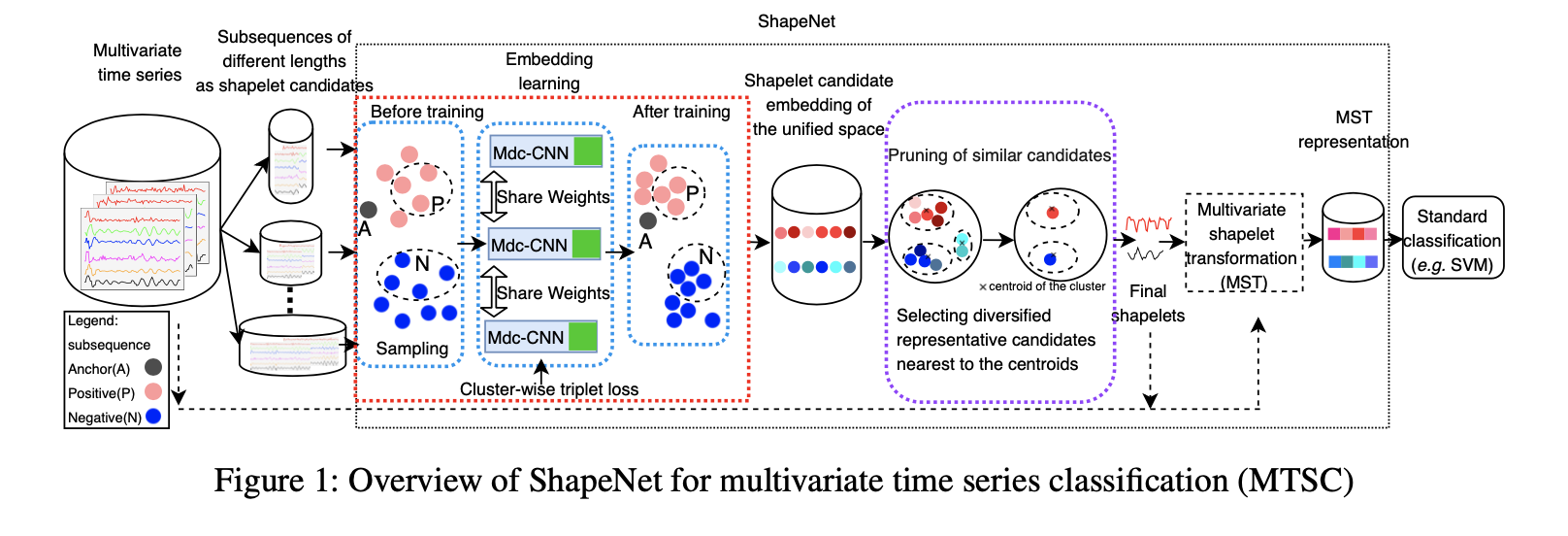
2 相关工作
MTSC的现有方法:基于模型和基于神经网络。
3 ShapeNet
在本节中,我们提出了一个Shapelet神经网络方法,即ShapeNet。 具体来说,我们提出了多长度输入的扩张因果CNN,聚类三元组损失函数和多变量小波变换。
3.1 Mdc-CNN
小波候选者最初是具有不同长度的所有时间序列子序列。 我们使用离散大小的滑动窗口(图1的圆柱体中显示的数据)来生成候选对象。 我们的目标是将所有小波候选者从原始空间嵌入到一个新的统一空间中。
3.1.1 设计原理。
首先,使用扩张的因果卷积神经网络(Dc-CNN)来学习时间序列子序列的新表示。已有研究证明了扩张因果关系网络对于序列建模任务的有效性。 扩张的卷积用于修改卷积的接受域。 因果卷积的设计使得将来的数据不会影响对过去数据的学习。
其次,尽管输出的长度可以与输入的长度相同,但是Dc-CNN无法处理各种长度的输入。 因此,我们建议引入一个全局最大池化层和一个线性层,它们堆叠在最后一个Dc-CNN层的顶部,以将所有小波候选者嵌入到统一空间中(图1中的绿色框表示)。 我们称其为多长度输入扩张因果CNN(Mdc-CNN)。
3.1.2 Mdc-CNN结构。
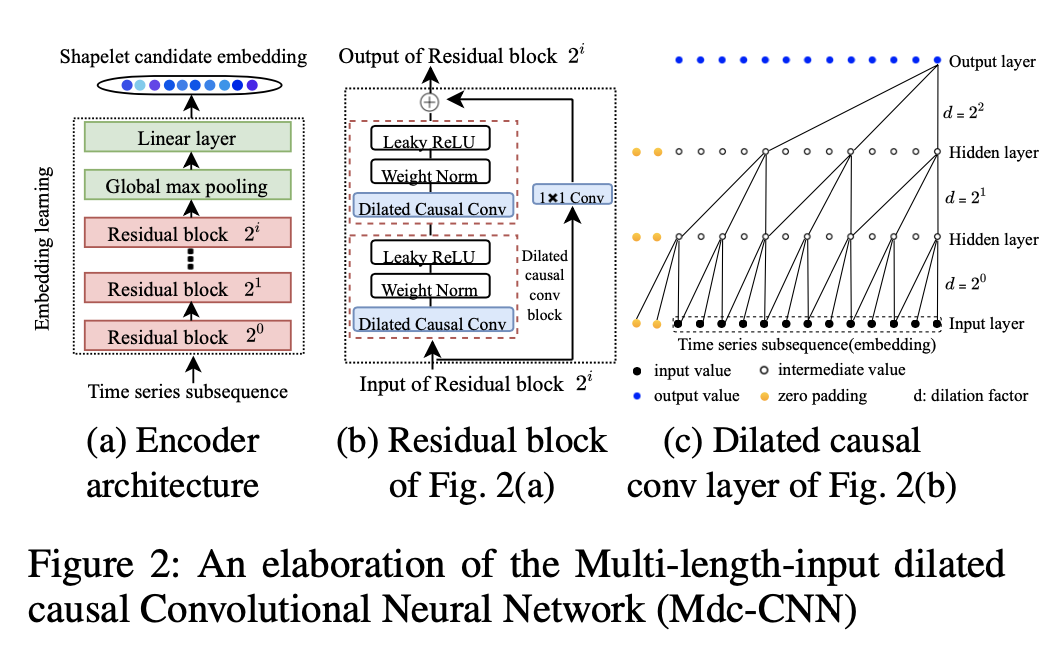
Mdc-CNN在图2中进一步说明。
图2(a)显示,编码器具有$i+1$层残差块,其中$2^i$是扩张因子,并且全局最大池化层和线性层堆叠在顶部的残差块。 编码器的输入是各种长度和变量的时间序列子序列,输出是它们的统一表示。 我们称输出小波候选嵌入。
图2(b)给出了具有两个相同子块的残差块,以及一个扩张因果卷积块。
图2(c)给出了一个扩张因果卷积示例,其扩张因子$d=2^0,2^1,2^2$。
3.2 无监督的表示学习
接下来,我们将说明如何以无监督的方式训练Mdc-CNN网络。word2vec的原理假设单词的表示应满足两个要求:(i)表示应接近其上下文。以及(ii)它应与那些随机选择的上下文相距较远,因为它们可能与原始单词的上下文不同。
学习/训练(类似于word2vec)的目的是确保相似的时间序列获得相似的表示。
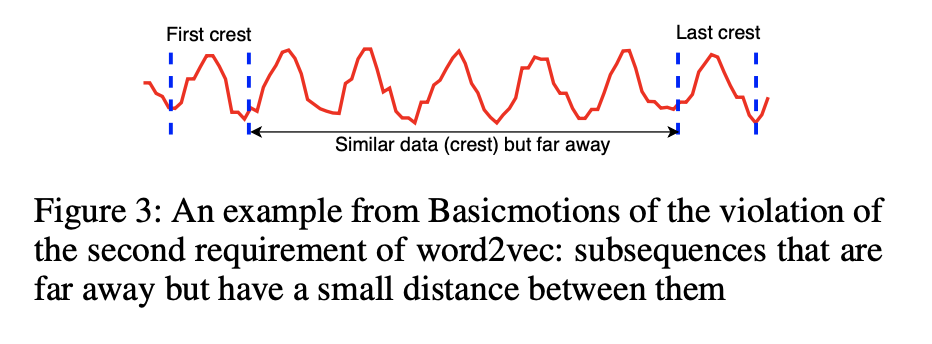
1.word2vec假设的第二个要求在时间序列中并不总是成立。 例如,Basicmotions数据集中行走类的一个变量如图3所示。我们可以很容易地观察到,波形的某些波峰很远但彼此之间并不遥远。
2.一批次中仅包含一个正样本来训练网络,在学习小波的表示形式时,这通常是不稳定的。
3.以前没有考虑过负(正)样本之间的距离。 图4显示了使用原始三元组损失学习小波表示的损失。 可以注意到,虽然损失略有下降,但它是不稳定的并且几乎不会收敛。
聚类三元组损失函数。 在本文中,我们提出了一个聚类三元组损失函数,该函数以多个正样本和负样本以及正样本(负样本)之间的距离作为输入。 为简单起见,我们采用两个群集来说明我们的损失函数。 具体来说,训练集$\mathcal{T}$中所有可能的三元组的集合定义如下:
其中x是锚定小波候选者,$x^+$和$x^-$分别表示大小为$K^+$和$K^-$的正样本和负样本的集合。
在某些真实的数据集中,三元组的数量很大,并且使用所有三元组进行训练在计算上是禁止的,并且次优。 所以,本文进行三重采样。
首先,我们将正(负)样本到锚点的归一化距离表示为$D{AP}(D{AN})$,我们具有以下公式:
其中,μ是在正样本和负样本之间强制执行的余量。 假设采用平方欧几里德距离。 然后可以如下定义$D{AP}(D{AN})$
$f(·)\in \mathcal{R}^z$是Mdc-CNN的嵌入表示形式,$z$是嵌入长度。
除了锚点与正(负)样本之间的距离之外,正(负)样本之间的距离也包括在内,并且应较小(较大)。 所有正(负)样之间的最大距离如下:
样本内损失定义如下:
将这些放在一起,我们为方程式中的模型建议三元组的聚类三元组损失函数(7),以无监督的方式训练网络。
示例1 图5中说明了等式7。在此示例中说明了我们的聚类三元组损失的两个群集。 三元组损失函数既可以使锚点与所有正样本之间的距离最小化,又可以使所有正样本(负)样本之间的距离最小化,并且可以使锚点(正样本)与所有负样本之间的距离最大化。
3.3 多元小波变换
在确定小波候选者的统一表示之后,我们建议选择高质量和多样化的候选者作为最终的小波。 最后,我们采用MTS的小波变换过程,然后应用经典分类器解决MTSC问题。
确定最终的小波。 通过遵循前面的小节,所有候选小波都被嵌入到一个统一的空间中。 它使我们能够简单地采用聚类方法(例如kmeans)来获得小波候选的Y个群集。 我们提出了一个效用函数(等式8)来对最接近聚类质心的候选进行排序。 等式8的第一个组件是候选小波集群的大小(大型群集意味着它代表许多候选者)。 第二个组件是候选小波与其他聚类中其他候选小波的距离(距离大表明候选小波与其他小波有所不同):
根据等式8在所有Y个群集中选择前k个候选对象,并检索原始时间序列子序列作为最终小波,表示为$S_k$。
多元时间序列转换
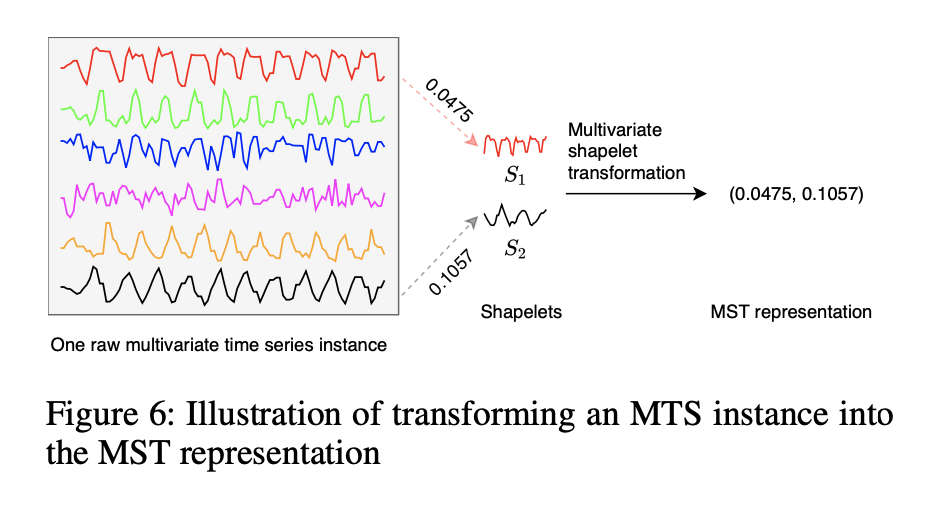
定义1 多元小波变换。 多元小波变换是通过使用一组最终小波$Sk$来计算距离将多元时间序列$\mathbb{T}_m$转换为新数据空间($d{m,1},…,d{m,k}$)的方法,表示为$d{m,j}=dist(T_m ^v,S_j)$,其中$S_j\in S_k,T_m^v \in \mathbb{T}_m$。并且它们的变量相同。
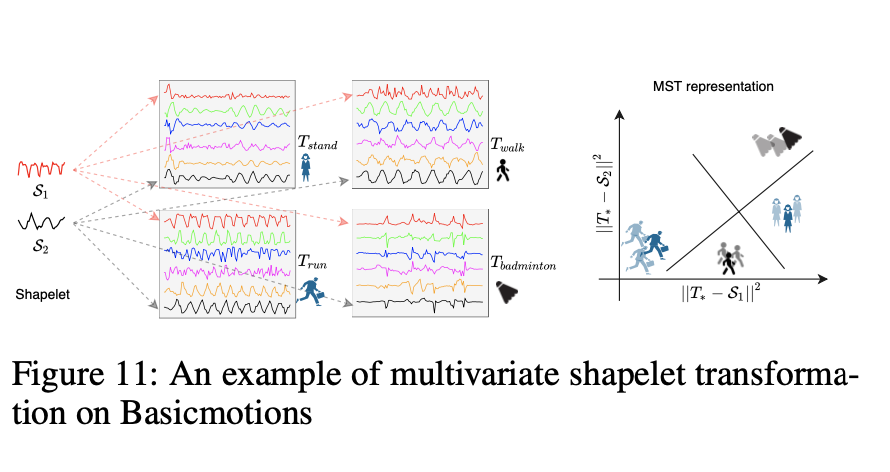
示例2 图6显示了一个MST示例。最左边的图显示了一个实例,其中包含Basicmotions数据集中的六个变量。 中间有两个小波 S1和S2。 对于MST,我们计算具有相同变量的时间序列子序列之间的距离(例如,第一个变量(顶部的红色时间序列)与S1之间的距离)。 因此,时间序列实例的MST表示是一个向量,如最右部分所示。
当所有MTS实例的转换完成时,可以利用某些标准分类器(例如SVM)从转换后的表示中学习分类模型。 在本文中,我们采用具有线性核的SVM,以便可以观察小波的权重进行分类。
4 实验内容
4.1 数据集和参数
测试了MTS数据集的著名基准,即UEA ARCHIVE。
批处理大小,通道数,卷积网络的内核大小以及网络深度分别设置为10、40、3和10。
学习率保持固定在$\eta=0.001$的较低值,而网络训练的时期数为400.等式1中$\mu=0.2$,对于三元损失函数中$\lambda=1$。 等式8中$\beta=0.5$。
4.2 Mdc-CNN的收敛性
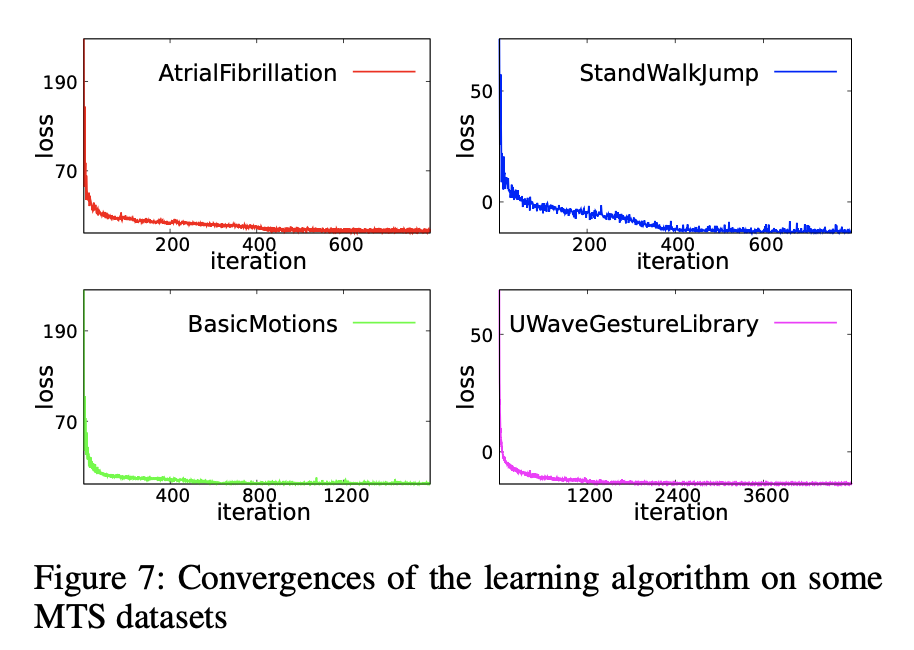
我们验证了Mdc-CNN的收敛性(取决于4.1中的参数)。 例如,学习算法在四个数据集上的收敛性如下图所示:
随着训练在所有四个数据集上进行,所有损失都非常平滑地收敛。 我们还可以观察到,损失在开始时迅速收敛,然后稳定下来。 从其余的数据集中可以观察到类似的趋势。 这验证了我们的集群三元组损失的有效性。
4.3 Baselines
我们将ShapeNet与七种不同的方法进行了比较。
·三个基准: 三种基准分类器(EDI,DTWI和DT WD)基于欧氏距离(EDI),与维度无关的动态时间规整(DTWI)和与维度有关的动态时间规整(DTWD)。
·MLSTM-FCN: MLSTM-FCN是一种深度学习框架。
·WEASEL-MUSE: WEASEL MUSE是基于模式袋的方法,具有统计特征选择,可变的窗口长度和MTSC的SAX。
·负样本(NS):该方法在训练其神经网络时应用了多个负样本,然后利用SVM进行最终分类。
·TapNet:TapNet是一种新颖的MTSC模型,带有注意力原型网络,可以利用传统方法和基于深度学习的方法的优势。
4.4 实验的准确性
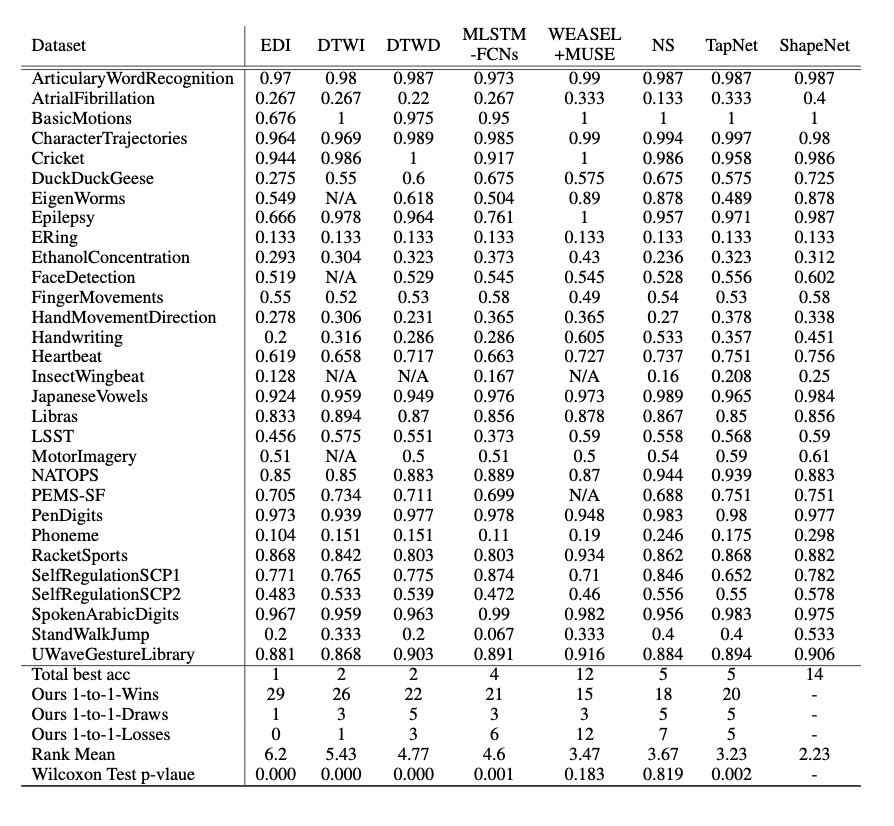
与其他方法比较。基线结果的实验准确度分别来自原始论文。 我们只考虑用于实验的标准化数据集。 表1给出了数据集的总体分类准确度结果。ShapeNet的准确度结果为10次运行的平均值,所有数据集的标准偏差均小于0.01。
从表1中可以看出,ShapeNet的总体精度是所有方法中最好的。 此外,ShapeNet在14个数据集中表现最佳,超过了其他三种基准测试方法。 ShapeNet的总最佳精度几乎是NS,TapNet,WEASEL-MUSE和MLSTM-FCN的两倍,并且显然比其他方法还要好。
弗里德曼检验和威尔科克森符号秩检验。
Friedman检验是一种非参数统计检验,用于检测八种方法在30个数据集中的差异。 我们的统计显着性是p = 0.00,小于α= 0.05。 因此,我们拒绝零假设,所以这八种方法之间存在显着差异。
我们注意到ShapeNet在所有比较方法中平均排名第一。 我们进一步针对所有基线进行了Wilcoxon检验,发现所有结果在p <0.05时均具有统计学显着性,除了表1最后一行中的WEASEL-MUSE,NS。
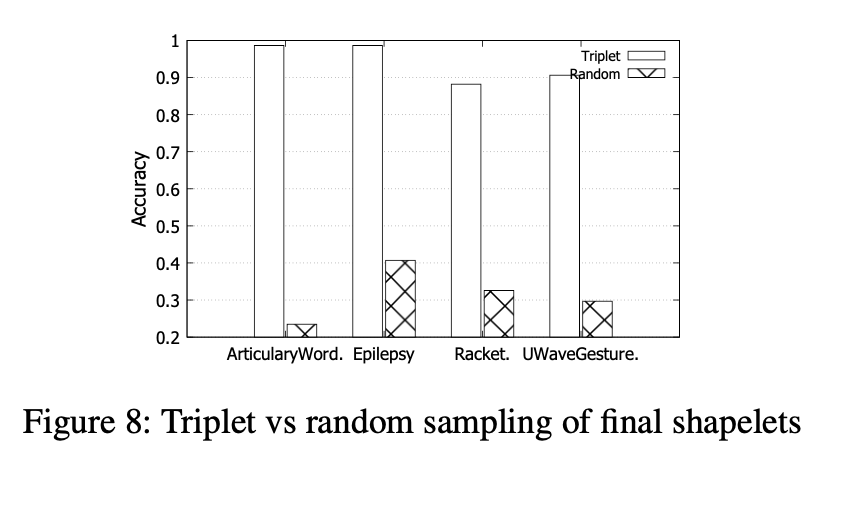
三重抽样与随机抽样。为了研究三重采样的性能,我们将其与随机三重采样进行比较以训练网络。 由于这里空间的局限性,我们在图8中仅显示了四个MTS数据集的结果,图8显示了最终精度的结果:我们的三元组采样显然是最好的。
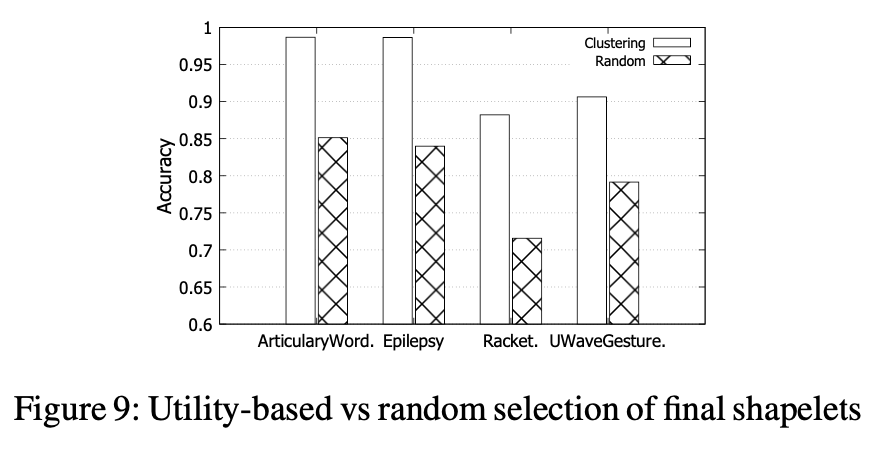
基于效用与随机选择。为了研究第3.3节中选择最终形状的效用函数的有效性,我们进行了一项实验,将其与随机选择进行比较。 聚类数为200,k的值为50。随机选择数为50。 它们如图9所示。在其他数据集中也可以找到相同的趋势。 在所有四个数据集中,我们基于效用的方法的准确性明显优于随机选择的方法,这表明它具有发现高质量小波的优越能力。
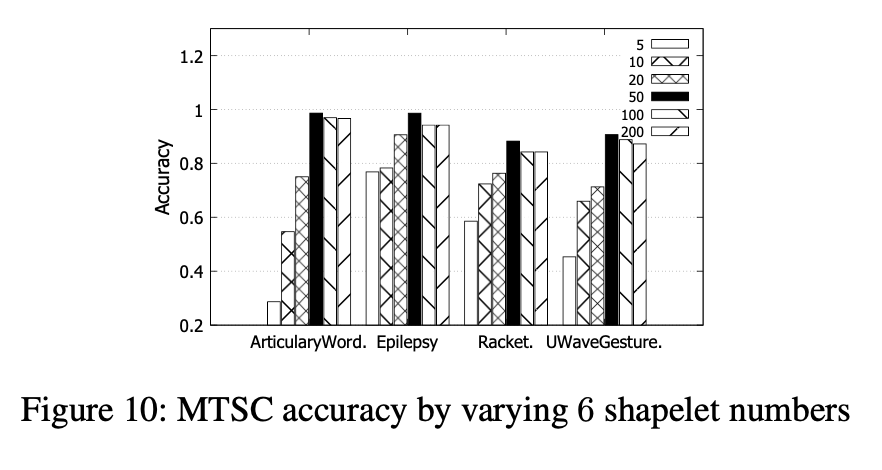
小波数量的变化。我们在四个MTS数据集上比较了200个聚类中不同数量的前k个小波对ShapeNet最终精度的影响。
图10显示了通过改变小波数的准确性。 在所有四个数据集中,随小波数量从5增加到50,精确度迅速提高,然后略有下降。
4.5 实验的可解释性
我们进一步研究了小波的可解释性,这是基于小波的方法的优势。 我们报告了ShapeNet从两个数据集中生成的两个Shapelet(即k = 2)。 选择这些数据集的原因很简单,因为它们无需太多领域知识即可呈现。
解释Basicmotions的小波
从图11中的Basicmotions数据集(最左侧的图)中发现了两个有趣的小波S1和S2。S1描述x轴的加速度,S2描述z轴的角速度。 ShapeNet从第一个和第六个变量中选择小波,这表明变量的重要性。 中间的图显示了来自数据集的四个类别的四个多元时间序列。 不同的颜色显示不同的变量。 距离只能在相同变量(在视觉上为相同颜色)的时间序列之间计算。 到两个小波的距离将多元时间序列投影到二维空间中(最右边的图)。 然后,通过线性分类器对转换后的表示进行分类。 结果表明,S2在区分羽毛球运动与其他运动方面是有效的。 S1可以区分步行和跑步。S1和S2都可以区分站立和其他运动。
我们注意到,与小数据相比,具有小波的MST表示更易于解释,并且可以观察到一些知识。 例如,站立和羽毛球的S1相似,这很直观。 事实证明,在等待羽毛球比赛时,很多球员都站了起来。
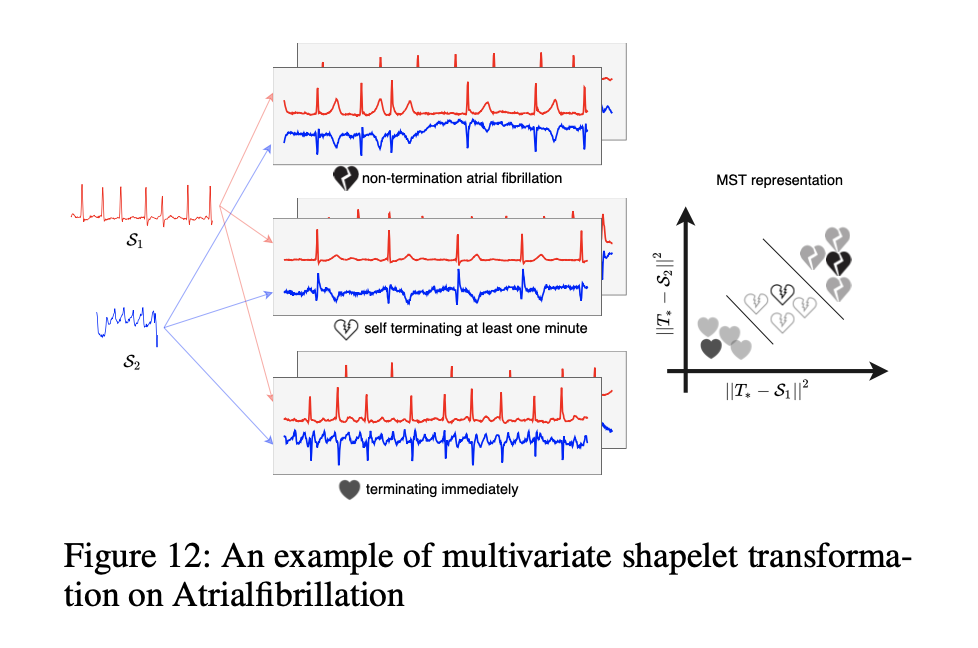
解释AtrialFibrillation(心房颤动)的小波
我们以AtrialFibrillation(这是一个带有两个变量的ECG数据集)为例,以显示发现的多元小波的可解释性。 数据集中有三类,即“持续性房颤”,“至少一分钟自终止性房颤”和“立即终止性房颤”。 它们分别标记为N,S和T。 从对AtrialFibrillation的简短描述中,我们可以知道这三个类别的终止时间为T <S <N。但是,即使以图解形式,原始数据也难以理解。 在图12中,我们的小波S1和S2将所有原始时间序列转换为二维空间。 在MST表示中,读者可以轻松地跟踪每个类别的终止时间。 新空间的大小越大,原始时间序列终止的次数就越多。
5 总结
本文提出了一种新颖的用于MTSC的小波神经网络方法ShapeNet。 我们提出了Mdc-CNN,以将各种长度的时间序列子序列学习到统一空间中,并提出了基于聚类(簇)的三元组损失,以无人监督的方式训练网络。 我们采用MST来获得时间序列的MST表示。 转换后,我们使用带有线性核的SVM进行分类。 实验结果表明,ShapeNet的分类准确性优于七个比较方法。 学习算法收敛迅速,效用函数有效。 小波的数量可以设置为50(默认情况下),以实现最高的精度。 小结的可解释性通过两个案例研究得以说明。 至于未来的工作,我们计划研究缺少值的MTS,这对于现实世界的数据集而言具有挑战性。