关键词:自监督学习,EEG,时间序列
Abstract
时间序列通常很复杂且信息丰富,但标记稀疏,因此很难建模。 在本文中,我们提出了一种自监督框架,用于学习非平稳时间序列的通用表示。 我们的方法称为时间邻域编码(TNC),它利用信号生成过程的局部平滑度来及时定义具有相似属性的邻域。 通过使用无偏差的对比目标(debiased contrastive objective),我们的框架通过确保在编码空间中来自邻域内的信号的编码特征与非邻域信号的编码特征是可区分的,来学习时间序列表示。 我们的动机来自医学领域,在该领域中,对时间序列数据的动态性质进行建模的能力对于在几乎不可能标记数据的环境中识别,跟踪和预测潜在患者的潜在状态尤其有价值。 我们将我们的方法与最近开发的无监督表示学习方法进行了比较,并证明了在针对多个数据集进行聚类和分类任务方面的卓越性能。
ICLR 2021
Sana Tonekaboni∗, Danny Eytan, Anna Goldengerg (University of Toronto & Vector Institute;The Hospital for Sick Children)
1. Introduction
由于时间序列的复杂性以及标签在真实场景下不可获得性,监督学习变得比较困难。采用无监督表示学习可以利用数据内在的结构特点,从原始序列中提取低维的、富含信息的表示,而无需监督信息。这些表示更加通用并且鲁棒,这是因为他们不是针对某个特定的监督任务提取的。无监督表示学习在CV, NLP上都有广泛的应用,但是在时间序列上面的研究还比较少。这种建模时间序列动态特性在医学领域是非常有价值的,因为健康检测数据通常表现为时间序列。
本文提出了一种自监督框架来学习复杂的多变量非平稳时间序列的表示,称为TNC(Temporal Neighborhood Coding),是专门为信号随着时间变换而变化的这种时序特征设计的,目的在于捕捉序列潜在的时序动态性。我们评估了在多个数据集上学习到的表示的质量,并表明学到的表示是通用的,可转移到许多下游任务,如分类和聚类。本文贡献主要体现在下面三方面:
- 针对非平稳多元时间序列数据,我们提出了一种新的基于邻域的无监督学习框架
- 我们引入了具有平稳性质的时间邻域的概率作为相似窗口在时间上的分布。利用信号的性质和统计测试结果自动确定邻域边界
- 我们引入正例的无标记学习(Positive Unlabel learning)的概念,具体来说是对非邻域的样本进行权重调整,以解释为对比损失在抽样负样本时引入的偏差
2. Method
我们提出一个自监督学习框架,学习一个表示空间,通过确保在表示空间中,可区分近端信号在时间上的分布与远端信号的分布。定义如下符号表示:
原信号:$X\in R^{D*T}$,$T$为序列长度,$D$为特征维数
时间窗:$X[t-\frac{\delta}{2},t+\frac{\delta}{2}]$ 表示以时刻$t$为中心,长度为$\delta$的窗口长度,也记为$W_t$
$W_t$的邻居集合:$N_t$, 是由以$t^$为中心,从一个正态分布$t^\sim \mathcal N(t,\eta·\delta)$采样得到。$\eta$是定义邻居范围的参数,描述了信号的统计特征如何随时间变化的特性,通常需要领域专家基于专业知识来确定。
$W_t$的非邻居集合:$\bar{N_t}$
我们的目标是:来学习$W_t$的潜在表示,再通过时间上的滑窗,我们可以获得信号潜在状态的变化轨迹。
基于这样的假设:利用信号生成过程的局部平滑性,将邻域分布特征刻画为高斯分布,对时域数据中的逐渐过渡进行建模,直观地,这些邻域样本(正样本)的表示与$W_t$的表示相似度大,而非邻域中的样本(负样本)和$W_t$的表示相似度小。
然而,这种假设可能会受到抽样偏差的影响,这是大多数对比学习方法中常见的问题。
在随机选取负样本的时候可能存在这样的情况,虽然“负样本”距离$W_t$很远,但是和参考样本很相似,有相同的隐含状态。例如,在存在长期季节性的情况下,信号可以在遥远的时间表现出类似的特性。
$TNC$由两部分组成:
- 编码器$Enc(W_t)$将$W_t\in \mathbb{R}^{D*\delta}$编码成更低维的空间$Z_t\in \mathbb{R}^M$
- 鉴别器$\mathcal{D}(Z_t,Z)$来估计$Z$在和邻域$N_t$内的概率。确切来说,它从编码空间中接收两个样本,并预测属于同一时间邻域的样本的概率。对于鉴别器$\mathcal{D}(Z_t,Z)$,我们使用一个简单的多头二进制分类器,如果$Z$和$Z_t$是邻居在时间上的表示,则输出1,否则输出0
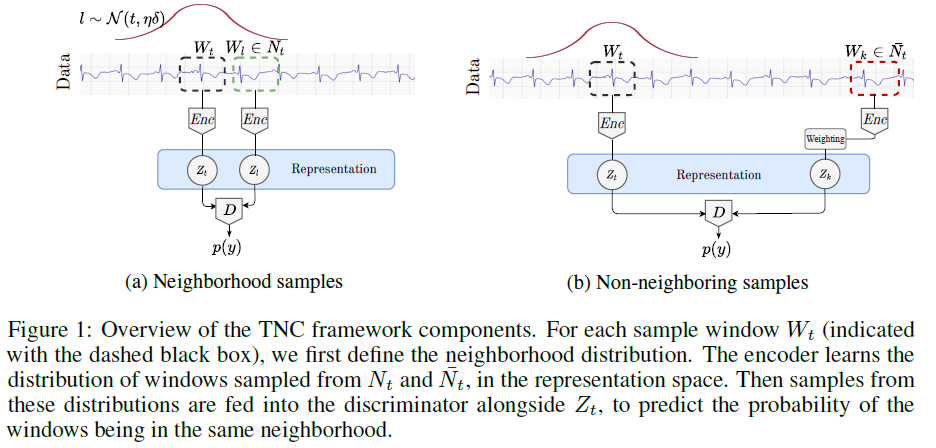
我们希望鉴别器的概率似然估计是准确的,即输入一对近邻样本的表示时概率接近于1,输入一对相聚较远样本的表示时概率接近于0。在非邻域$\bar{N}$内,为了缓解上面提到的负样本抽样偏差问题,采用权重系数$w$来调整非邻域内的正样本。
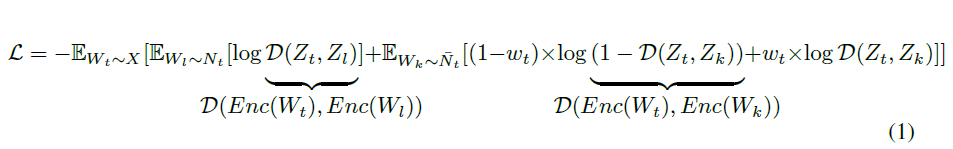
我们通过优化这一目标,同时训练编码器和鉴别器。注意,鉴别器只是训练的一部分,不会在推理过程中使用。
- 确定$\eta$值
ADF-test ——可用于验证时间序列的平稳性假设
由于邻居样本代表相似的样本,我们需要确定$\eta$合适的值,使得在一个平稳信号生成过程中,应该能识别出这个相似时间跨度的样本分布。这里采用ADF test(Augmented Dickey-Fuller)自动根据信号本身的行为对每个时间窗确定$\eta$的范围。$\eta$太小,邻域内的许多样本会重叠,使得编码器学习到的信息都是重复信息;如果$\eta$太大,领域可能跨越多种潜在状态,使得编码器也学不到不同状态之间的变化,因此无法区分。
我们将每个窗口周围的时间邻域定义为信号相对平稳的区域。由于信号可能会在一段未知的时间内保持潜在状态,因此每个窗口的邻域范围$\eta$可能在大小上有所不同,必须根据信号的行为进行调整。为此,我们使用ADF-test得出邻域范围的统计检验。
- 负样本抽样偏差的问题
PU learning(Positive Unlabeled learning)——在只有正例和无标记样本的情况下训练一个二分类器
如上提到的偏差问题,我们考虑在$N_t$内的样本都和当前参考样本$W_t$相似,视为已知的正样本,但在的样邻域外的样本不一定和$W_t$不同。我们将非邻域样本视为 Unlabeled data。因此有两种策略去解决unlabeled data:1. 把所有无标签样本都视为负样本;2. 把无标签样本视为带更小权重的负样本。在第二种策略下,无标签数据在损失项中需要被赋予适当的权重,才能去训练一个无偏的分类器。
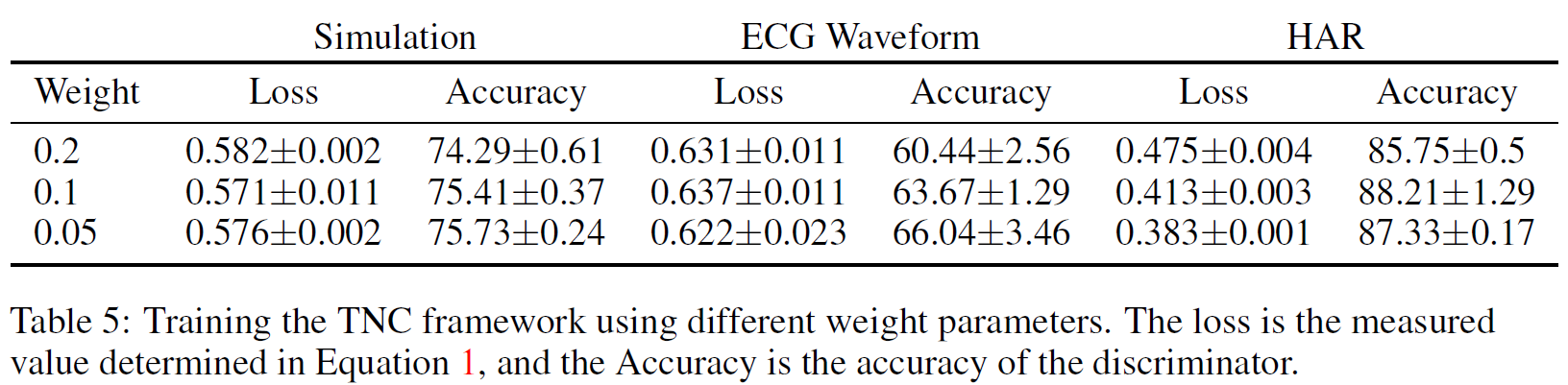
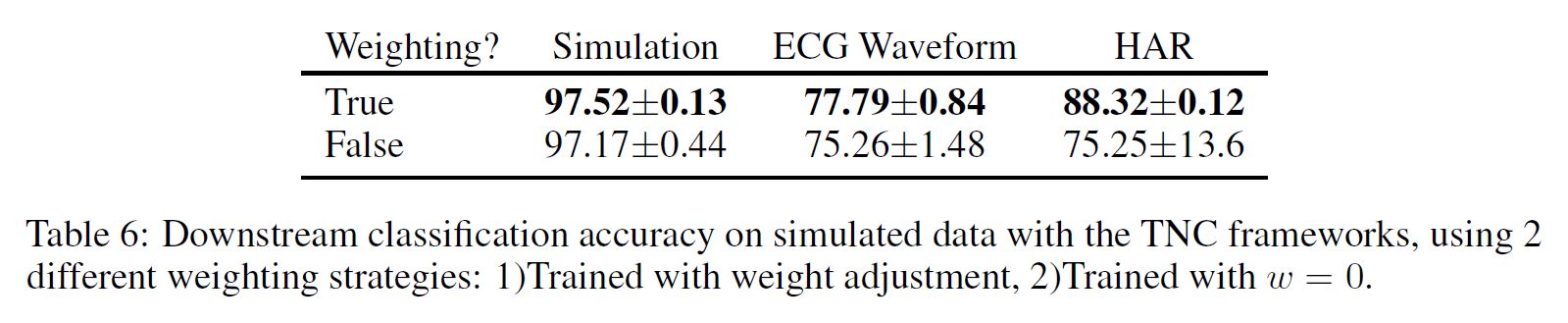
在TNC框架中,这个权重$w$指的是$\bar{N_t}$中样本与$W_t$的相似样本出现的概率。附录A.6解释了如何为我们不同的实验设置选择权重参数,也演示了权重调整对下游任务性能的影响。
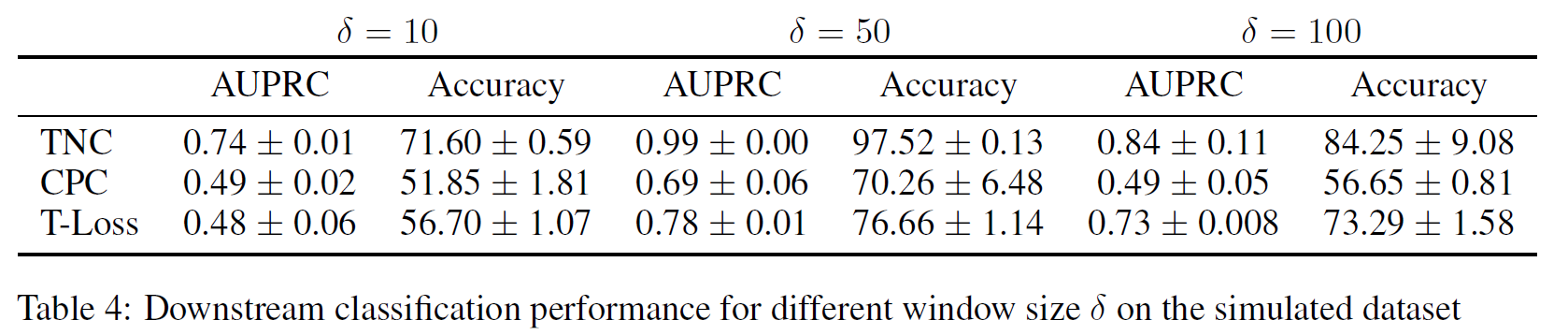
窗口大小选择的影响:
无偏损失系数$w$的影响
完成邻域分布的定义后,我们训练目标函数来鉴别邻域内样本的表示和邻域外样本的表示。理想的编码器完成编码后,得到的编码空间保留了邻域内样本的特性。设$Z_l=Enc(W_t),W_l\in N_t,Z_k=Enc(W_k),W_k\in \bar{N_t}$
3. Experiment
我们在多个时间序列数据集上评估我们的框架的可用性,这些数据集具有随时间变化的动态潜在状态。我们将时间序列的分类性能和可聚类性与两种最先进的无监督表示学习方法进行了比较:1.对比预测编码(CPC) ,使用预测编码原则训练编码器的概率对比损失。2. triplet - loss (T-Loss),它采用基于时间的负采样和triple - loss来学习时间序列窗口的表示。triplet-loss 的目标是通过最小化正样本(子序列)之间的距离,同时最大化正样本与负样本之间的距离,确保相似的时间序列具有相似的表示。
为了公平比较,确保最后的性能差异不是模型的结构造成的,本文在所有baseline中用一样的Encoder网络,因为我们的目标是比较学习框架的性能,与编码器的选择无关。我们通过1)评估编码空间的聚类性和;2)使用下游分类任务的表示来评估表示的泛化性。
除了上述baseline,还有基于DTW的K-means/KNN
Datasets
Simulated data
采用HMM生成随机隐含状态,在每个状态,时间序列又由不同的过程生成如不同核函数的高斯过程,非线性自回归移动平均模型,最终生成的序列包含3个特征的2000个测量值,包含4个不同的隐含状态。我们使用了一种双向、单层递归神经网络作为编码器
Clinical Waveform Data
MIT-BIH Atrial Fibrillation dataset。该数据集包括25个患有房颤的人类受试者的长期心电图记录(持续10小时)。它由两个心电信号组成,每个都以250hz采样。随着时间的推移,信号被标注为4类不同类型的心律。本实验的目的是在没有任何标签信息的情况下确定每个样本的潜在心律失常类型。
由于简单的RNN结构不能建模高频的ECG信号,因此,这里采用6层CNN结构作为编码器。窗口大小设为2500个点,编码的表示为64维的向量。
Human Activity Recognition (HAR) data
利用加速度计和陀螺仪测量的时间数据来预测活动类型。数据集包含30个个体,每个人监测6种活动。单层RNN编码器作为编码器。窗口设为4,代表15s的记录,编码的向量10维。
4. Results
这里评估了所有baseline再所有数据集上的可聚类性能和下游任务上的分类性能。可群集性表示每种方法恢复原先状态的良好程度,而分类则评估我们的表示对下游任务的信息量有多大。
4.1可聚类性
许多真实世界的时间序列数据具有底层的多类别结构,这自然导致了具有集群属性的表示。如果隐含状态的信息被编码器充分学到了,那具有相同隐含状态的信号编码后应该能聚集在一起。
下面是针对仿真数据,利用三种不同的框架学习到的隐空间的特征表示可视化结果:
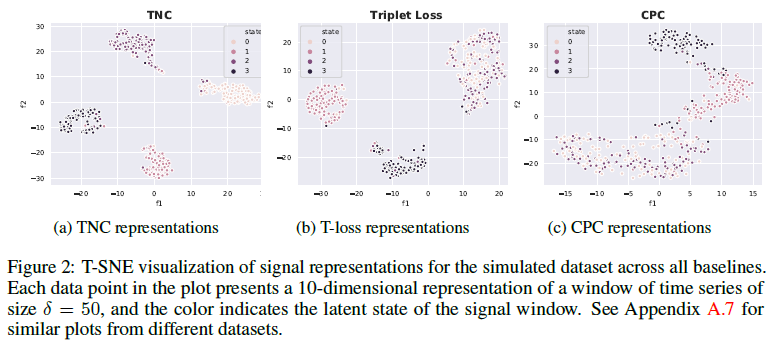
为了比较每个baseline聚类的一致性,我们使用两个常用来衡量聚类有效性的指标:Silhouette score$\in[-1,1]$,分数越高代表聚集性越好;Davies-Bouldin index,衡量类内相似性和类间差异,分数越低代表聚集性越好。我们在表示空间中使用K-means聚类来度量这些可群集性得分。
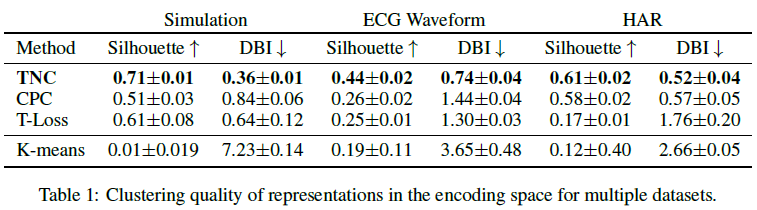
TNC:在所有baseline和数据集上都取得了最好的得分,可聚集性表现最好
CPC:HAR数据集,CPC可以很好地对状态进行分组,因为大多数活动都是按照特定的顺序记录的,增强了预测性编码。在ECG波形数据上的表现接近于Triplet-loss,但在模拟数据集上表现较差,因为模拟信号是非平稳的,而且过渡难以预测
Triplet-loss:在模拟环境中表现良好,但无法区分状态0和状态2,可能原因是其中信号来自不同参数的自回归模型
4.2 分类性能
我们训练一个线性分类器来评估使用表示来分类隐藏状态的效果如何。所有baseline的性能与监督分类器进行比较,监督分类器由一个编码器和一个与无监督模型具有相同架构的分类器组成,以及一个使用DTW度量的k近邻分类器。评价指标:AUPRC(area under the precision-recall curve),因为对于不平衡分类设置,如波形数据集,AUPRC可以更准确地反映模型性能。
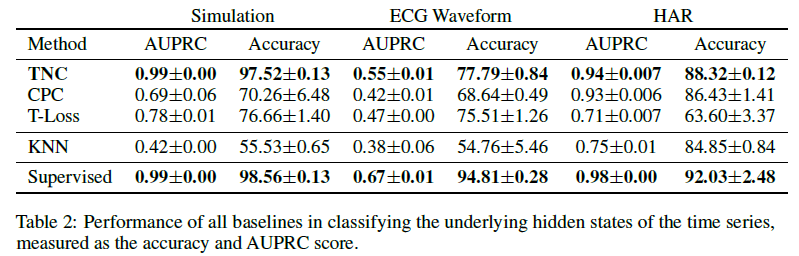
TNC接近端到端有监督模型的分类效果。这进一步证明了我们的编码捕获了时间序列的信息部分,并且可泛化用于下游任务。
对于HAR这样的数据集,时序内部的状态更替存在一定的顺序性,因此CPC能取得较好的结果。而当时序中增加非平稳性后,性能就下降了。CPC和triple Loss方法性能相对较低也可能是因为这些方法都没有明确解释当随机选择的负样本时,仍然得到和参考样本$W_t$相似的信号段从而造成抽样偏差。
4.3 trajectory
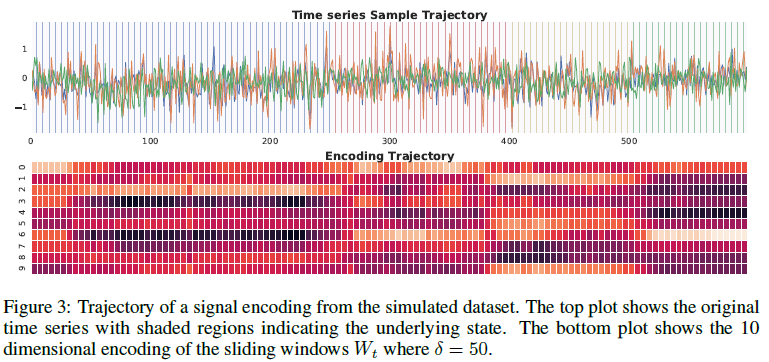
上面部分是原始序列,下面是编码序列,阴影部分表示一种隐含状态。原信号的状态转换也体现在编码特征。
5. Conclusion
本文提出了TNC(Temporal Neighborhood Coding)框架,来学习非平稳,多变量时间序列的状态表示。文章的出发点是在医疗保健领域,学习丰富的时间医学数据表示对于了解患者的潜在健康状况变化非常重要。然而,现有的大多数表征学习方法都是针对特定的下游任务而设计的,需要专家进行标记。本文在多个数据集上验证了TNC学到的表示是通用的,灵活可扩展的。因此这一框架也可以用于其他数据领域。同时也可以将这种表示学习方法应用到多种下游任务比如异常检测。