题 目:一种严格的对于时间序列可解释性的评估方法
出 处:ICCV2019
关键词:时间序列,可解释性
可解释的人工智能(XAI)方法通常被用于解释和调试黑盒机器学习模型。然而,大多数提出的XAI方法都是黑盒本身的,并且是为图像设计的。因此,他们依靠视觉上的可解释性来评估和证明解释。在这项工作中,我们应用了以前用于时间序列上的图像和文本域的XAI方法。我们提出了一种方法来测试和评估时间序列上的各种XAI方法,通过引入新的验证方法来纳入时间维度。我们进一步进行了初步实验,以评估在一系列数据集上使用各种验证方法对所选择的XAI方法解释的质量,并对其进行质量指标的检查。我们证明,在我们最初的实验中,Shap对所有模型都很有效,但其他模型如DeepLIFT、LRP和显著性地图在特定架构中工作得更好。
1. 引言
由于深度学习在很多领域先进的表现,这种复杂模型的可解释性引起了越来越多的兴趣。机器学习系统的需求(公平性、隐私性、可靠性、信任构建)为模型提供了一个新的选择过程。
许多突出的XAI方法都是针对特定的输入类型而定制的,例如:图像=>显著性图,文本=>LRP。然而,例如,视频(图像序列)和音频有另一个时间维度,这是目前被XAI方法省略的。目前,XAI对时间序列数据的研究非常有限。然而,由于传感器越来越便宜,除了视频和音频之外,还会产生更多面向时间的数据,因此,首先测试已经突出的XAI方法和发现新的方法是很重要的。
因为原始时间序列很大,即使是领域专家自己也难以解释,因此通过原始数据进行评估和解释检查是不可行的。由于缺乏可连接的领域知识,需要一种可量化的方法来验证解释。在计算机视觉中存在一些关于评估可解释性的工作(例如,将相关像素设置为零),这也可以在时间序列上使用。然而,这些方法通过假设特征独立性或仅局部(短期)依赖来省略时间依赖。因此,需要对先前方法的适应或新的变体来评估对时间序列的解释。
2. 时间序列可解释性
时间序列D的分类数据集,包括属于k个类$c{1}, c{2}, c{3}, \ldots, c{k}$。的n个样本。每一个样本t由m个时间点组成$t=\left(t{0}, t{1}, t{2}, \ldots, t{m}\right)$
对大多数XAI方法通常考虑的解释是局部特征的重要性,时间点转换为特性,以引入在时间序列上使用XAI方法的解决方案。局部特征的重要性产生了对每个时间点ti的相关性ri,然后可以建立一个时间序列向量$t=\left(t{0}, t{1}, t{2}, \ldots, t{m}\right)$对应的一个相关向量$r=\left(r{0}, r{1}, r{2}, \ldots, r{m}\right)$。
模型m从D的子集X以及标签Y训练得到。模型m根据给定的数据X,Y进行训练,并用于新的子集Xnew的预测。在时间序列任务中,x是一个由m个时间点组成的样本$t=\left(t{0}, t{1}, t{2}, \ldots, t{m}\right)$,一个可解释性方法可以被定义为$x a i(x, m)=e x p$,其中exp是指事后解释。对于时间序列,exp往往是指m个时间点的相关性$r=\left(r{0}, r{1}, r{2}, \ldots, r{m}\right)$。
与图像上的显著性图类似,可以基于相关性创建一个热图,可以用这个热图来丰富原始时间序列的线形图来创建一个可视化。与领域知识一起,专家可以检查所产生的解释可视化,以定性地验证结果。
使用的数据集是FordA时间序列集,模型使用的是ResNet。
FordA任务中每条数据是包含500个汽车发动机噪音测量值的时间序列,基于这个时间序列来判断汽车发动机是否有问题。
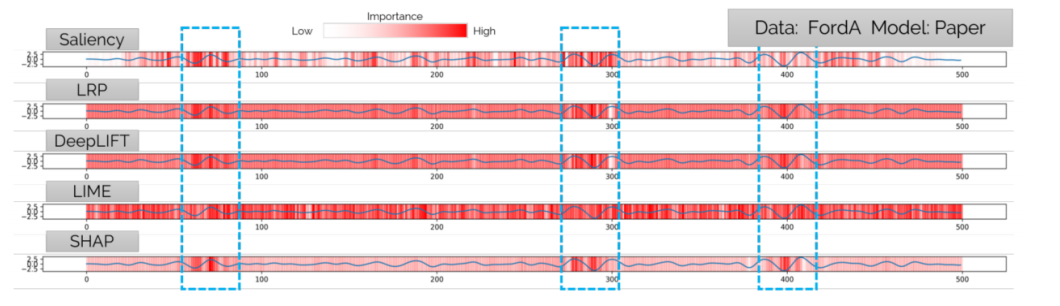
上图中,蓝色曲线表示为选取的一条FordA数据,红线表示数据中每个点的特征重要度。
红线颜色越深表示该点的特征对于输出影响越大,红色越浅表示影响越小。
上图中三个蓝色框标记的数据点表示为对输出有明显影响的特征,SHAP、LRP和DeepLIFT三种算法对于这类特征有明显的划分。
LIME:一种和模型无关的局部可解析性算法。
Scaliency Maps: 基于反向传播梯度生成heatmap,显示输入像素对于输出的影响。
LRP: 基于反向传播relevance score生成heatmap。(主要用于图像领域,目前有不少nlp方向的应用)
DeepLIFT: 一种改进的基于反向传播梯度生成heatmap的算法。
SHAP: 基于博弈论shapely值计算特征的重要度。
3. 评估时间序列的可解释性
关于如何自动评估和验证XAI解释,有多种方法。在计算机视觉中,一种常见的方法是扰动分析。这种分析方法根据图像的重要性(最大或最小相关像素)替换图像的几个像素。考虑到面向时间的数据的序列特性,我们提出了两种明确适用于时间序列的新方法。
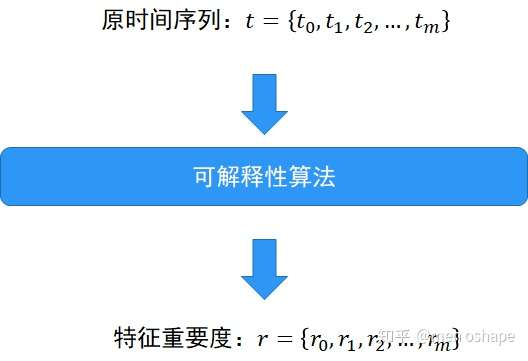
a. 首先通过可解释性算法计算时间序列中每个时间点ti对应的特征重要度ri:
b.扰动时间序列:Pertubation on time series

c.基于时间序列特征的扰动方法:
在b中两种对于时间序列的扰动方法并不能保证对输出会有很大的影响。
如果模型能学到时间序列上的波动趋势,那么仅扰动离散的几个时间点,并不能保证随机扰动和有选择扰动两种方式对于输出的影响有很大的差异。
由此,作者又提出专门针对时间序列特性的扰动方法:
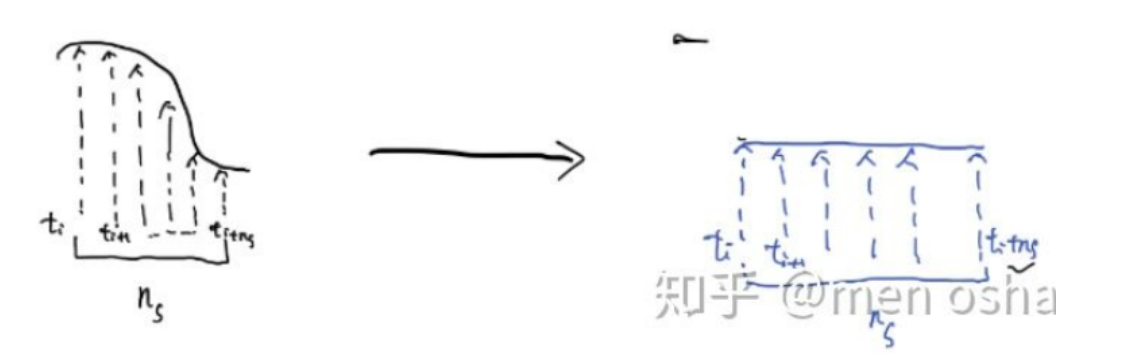
swap time points:选取扰动时间点ti周围ns个时间点作为一个需要扰动的时间子序列,将其逆序插回原来的时间序列。

mean time points: 选取扰动时间点ti周围ns个时间点作为一个需要扰动的时间子序列,取其平均后插回原来的时间序列。
4. 实验结果

分别实验了5种可解释性算法在3种模型上的效果,其中分别用4种扰动方法比较准确率的波动。
CNN:在都使用CNN模型的情况下,基于LRP和DeepLIFT算法的扰动效果最好。
RNN:在都使用RNN模型的情况下,基于Saliency和SHAP算法的扰动效果最好。
ResNet:在都是用ResNet模型的情况下,基于SHAP算法的扰动效果最好。
综上所述:
(1)作者认为SHAP算法鲁棒性最强,在解析各种模型时都有较好的效果。
(2)基于LRP和DeepLIFT这类基于反向回传的可解性算法在cnn模型表现更好。
(3) LIME算法在解析各类模型时表现最差。
(4)使用swap和mean扰动时间序列时,更能区分随机扰动和选择性扰动的效果。